The Photoelectric Effect - Light as a Particle

In two of my previous posts, here and here, which talk about blackbody radiation and ultraviolet catastrophe, the radiation is described in terms of the physics of waves.  However, this is not the only way that light can be described. Consider the following...

In the above, light is being shone onto the metal plate (A) and a voltage (V) is applied between the the metal plate (A) and the cup (B). If the cup and the plate are made of the same material the the voltage measured by the volt meter is the same as the voltage between the plate and the cup. The light that is being shone onto the plate releases some electrons, and therefore the ammeter measures a current flowing. This effect is the photoelectric effect. The diagram of the apparatus may not be clear therefore is it worth pointing out that that there is no physical connection between the plate and the cup, hence the ammeter is measuring what is called a photoelectric current.

The above graph shows the typical results produced by such an aparatus, it shows the photoelectric current as a function of the applied voltage. The two lines on the graph represent the results obtained for two different intensities (brightness) of light shone upon the plate. In both set of results, if the voltage is made large enough the current reaches a maximum value and further increases in voltage produce no further increase in current. At this point the cup is collecting all of the electrons which are released by the plate. 

If the voltage is reversed using the switch in the circuit some current will still flow, even through the voltage applied opposes the flow of the emitted electrons. This must mean that the electrons are released from the plate with an amount kinetic energy. However, it can be seen that if the reversed voltage is made large enough the current measured reduces to zero and it can also be seen that the voltage at which the current falls to zero is the same for both lines on the plot, where the two line represent results that would be obtained for two different light intensities. The voltage at which the current falls to zero, is called the stopping potential, and if this voltage is multiplied by the charge of an electron, the result gives the kinetic energy of the fastest electron emitted from the plate.

$$K_{max} = eV_0$$

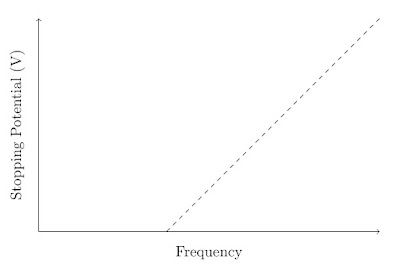
This shows that the stopping potential is independent of the intensity of the light used. However, the stopping potential does depend upon the frequency of the light used. The representation below shows the typical behaviour found when the frequency of the light is varied and the stopping potential found

Therefore, for a given plate material, a linear relationship above a certain frequency is obtained, however, there is a cut off frequency below which no photoelectric effect occurs. This characteristic is produced no matter what the plate is made of.

There are three aspects of this effect that classical wave theory cannot explain:

1. Wave theory requires that as the intensity of the light increases so does its electrical fuel strength, E. If the lights electrical field strength increases then the force of the electron, eE. Thus, as intensity of the light increases, the force on the electron should get higher, an thus the kinetic energy which which the electron is emitted should get higher. However, this is at odds with the experimental results which suggests that the kinetic energy of the fasted electron emitted eV_nought is independent of the intensity of the light used.
2. According to wave theory, the photoelectric effect should occur no matter what frequency of light is used provided that the light is intense enough to eject the electron from the plate. However, the experimental results for any given surface there is  frequency below which the photoelectric effect does not occur, a cut-off frequency, no matter what intensity of light is used.
3. In classical theory the light energy is uniformly distributed across its wave front and the area over which this energy can be absorbed by the electron is a circle having an atomic diameter. Thus if the light of low intensity is used there should be a time delay between the moment that light is shined upon the plate and the production of current. That is, it should take the electron a measurable amount of time to absorb the light energy provided to it. However, no detectible time delay has ever been recorded while studying the photoelectric effect. 

So it wave theory cannot explain these aspects of the photoelectric, what theory can?

Well, a very famous theoretical physicist came up with a theory (for which he surprisingly won the Nobel prize in physics although he is very much more well known for two of his other theories) that explains all of the aspects above, Albert Einstein, and it was his theory of the photon, a particle of light.  This other method that can be used to explain the behaviour of light will be the subject of my next post.

Resolution of the Ultraviolet Catastrophe

In my last post I explained the origins of what is called the ultraviolet catastrophe, the failure of classical physics to correctly predict the signature of blackbody radiation. In this post I will attempt to explain how this catastrophe was resolved, however, if I'm wrong, then please do leave comment below. 

The Rayleigh-Jeans formula, which gives the energy per unit volume (energy density) of blackbody radiation emitted inside a cavity which has been heated to a temperature T in the frequency interval \(v\) to \(v + dv\) is proportional to v squared
$$\rho_T (v)dv=\frac{8\pi v^2kT}{c^3}dv$$Hence this equation predicts that the higher the frequency of the radiation emitted, the higher its energy density should be. Whereas the experimentally observed energy density signature of blackbody radiation as a function of frequency for a given temperature does not continually grow with increasing frequency, rather it peaks and then falls back. The graph below illustrates this discrepancy, with the results from the Rayleigh-Jeans formula given by the dashed line and the solid line is the experimental results for a Temperature of 1500K

So how is the above catastrophe resolved...

Classical physics tells us that for a system with many entities which are in thermal equilibrium at temperature T, their kinetic energies will have a specific distribution, the Boltzmann distribution. For which the average kinetic energy per degree of freedom is given by 1/2kT, where k is Boltzmann's constant. Thus according to classical physics, the average kinetic energy of the waves of thermal radiation being emitted from the internal surface of a cavity, the cavity having been heated to a temperature T, is given by this equation - each wave is in thermal equilibrium with every other one and they only have one degree of freedom, the amplitude of their electric field. A common property of physical systems is that their total energy is twice their kinetic energy, thus each of the waves of the thermal radiation has the average total energy:

$$\bar\epsilon = kT$$

This equation tells us that each wave has the same average total energy, and the value is independent of frequency. If fact, this equation is an integral part of the Rayleigh-Jeans formula that gives the energy density of the thermal radiation. It is simply the product of the average total energy of each wave, as given above, multiplied by the number of waves of radiation that can fit within the cavity within the frequency interval \(v\) and \(v + dv\). 

From the graph above it can be seen that for waves that have small frequencies, the prediction of the Rayleigh-Jeans formula and the experimental results are in close agreement, that is, a wave's average total energy tends to \(kT\) as its frequency tends to 0

\(\bar\varepsilon \xrightarrow [\ v \rightarrow 0]{}kT\)  (1)

However, the experimental results show that the average total energy of the waves tend to zero as their frequency tends to very high values, that is

\(\bar\varepsilon \xrightarrow[\ v \rightarrow \infty]{}0\)  (2)

From these two tendencies it is clear to see that the average total energy of each wave is, in fact, dependent upon its frequency, that is each wave does not have the same total energy.

To determine the actual energy of each wave it is necessary to look at how the \(\bar\varepsilon=kT\) result is determined.

$$P(\varepsilon)=\frac{e^{-\varepsilon/{kT}}}{kT}$$

The above equation characterises a special form of the Boltzmann Distribution, where \(P(\varepsilon)d\varepsilon\) is the probability of finding a body of a system with an energy within the interval \(\varepsilon\) to \(\varepsilon + d\varepsilon\), where the number of states for that body within the interval is independent of \(\varepsilon\). Using this function, the average total energy \(\varepsilon\) can be found as follows:

$$\bar\varepsilon=\int_0^\infty \varepsilon P(\varepsilon) d\varepsilon$$

As carrying out an integral is simply determining the area under a graph, it is worth considering the function \(\varepsilon P(\varepsilon)\) graphically:

It was the great scientist, Planck, who first realised that the relationship between \(\varepsilon\) and \(v\) as set out by (1) and (2) could be achieved by treating \(\varepsilon\) as a discrete variable rather than a continuous one, that is by assuming that the energies within the energy distribution of the wave can only have discrete values, that is

$$\varepsilon=0,\Delta\varepsilon,2\Delta\varepsilon,3\Delta\varepsilon,4\Delta\varepsilon...$$

The effect of treating \(\varepsilon\) as a discrete variable rather than a continuous variable can be seen for small and large values of \(\Delta\varepsilon\) in the following graphs

Where \(\Delta\varepsilon\) is small, the area under the graph (shaded) is very similar to that where \(\varepsilon\) is treated as a continuous variable, that is the area tends to \(kT\). Where \(\Delta\varepsilon\) is large the area under the graph falls below that where \(\varepsilon\) is treated as a continuous variable. It is easy to see that as \(\Delta\varepsilon\) is made very large the area under the graph tends to 0, that is

$$\bar\varepsilon \xrightarrow[\ \Delta\varepsilon \rightarrow 0]{}kT$$

$$\bar\varepsilon \xrightarrow[\ \Delta\varepsilon \rightarrow \infty]{}0$$

These two tendencies are very similar to the tendencies set out by (1) and (2), in fact they can be related by simply stating that: 

$$\Delta\varepsilon \propto v$$

To convert this from a proportionality to a relationship a constant of proportionality, \(h\), is required. This constant is the well known Planck's constant.

Thus the Ultraviolet catastrophe is resolved by assuming that waves of blackbody radiation can only have discrete values of energy within their energy distribution, and that the discrete values of energy are a dependent on the wave's frequency. These concepts were used by Planck to derive his blackbody spectrum formula

$$\rho_T (v)dv=\frac{8\pi v^2kT}{c^3} \frac{hv}{e^{hv/kT}-1}$$

The derivation of this formula will be the subject of a separate post.

Blackbody Radiation and the Ultraviolet Catastrophe

So here it is, the promised post on the ultraviolet catastrophe.

The eagle-eyed amongst you have of course noticed the that title of this post also refers to blackbody radiation. Well the ultraviolet catastrophe cannot really be explained without first explain what blackbody radiation is. So here goes...

Blackbody radiation is simply a type of thermal radiation that is given off by certain types of materials, ones that absorb all thermal radiation they are exposed to, and reflect none of it. As it is the radiation that is reflected by a material that defines its colour, these materials have no colour, that is, they are black, hence their name. They are called blackbodies.

It is common experience that when items are heated, they glow, they emit radiation and not just radiation that we can see, they emit radiation across the whole spectrum. The signature that is emitted depends upon what the material is made of, however the signature of the radiation emitted by all blackbodies is identical, regardless of the material they are made.

The above graph gives the signature of blackbody radiation for a blackbody at three different temperatures 1000K, 1500K and 2000K as a function of frequency of the radiation emitted. The value  on the y-axis, RT(v), is called spectral radiancy, which is defined such that RT(v) dv is equal to the energy emitted per unit time in radiation of frequency within the interval v to v + dv from a unit area of the surface at a temperature T. 

Other than objects which have no colour, there are other entities that can behave as if they were blackbodies. One example is a hollow object which has a very small hole leading to the void inside of it. Radiation incident upon this hole will be wholly absorbed if the internal surface area of the void inside the object is large compared to the size of the hole. Thus, if the hole absorbs all thermal radiation that happens to be incident upon it, then it is behaving exactly as if it were a blackbody.

It is not too much of a leap from the behaviour explained above to see that if the objected is heated some of the thermal radiation emitted from the surface of void will pass through the whole and therefore this emitted radiation will bear a blackbody signature - the hoe acts as a blackbody. However, as the radiation emitted through the hole is just a sample of the thermal radiation inside of the void, then the thermal radiation inside the hole must also bear a blackbody signature. 

So, there you go, blackbody radiation in a nutshell. So where does the ultraviolet catastrophe fit into all of this. Well it comes about in efforts to predict the the signature of the blackbody radiation.

Using classical arguments (which I will go through in a future post) the following equation is arrived upon which should predicted the signature of blackbody radiation

This equation is called the Rayleigh-Jeans formula for blackbody radiation. It gives the energy per unit volume of the cavity at temperature T in the frequency interval v to v + dv. It can be seen that the energy density, as calculated by the above equation, is dependant upon the square of the frequency of the radiation, and as such, as the frequency increases the calculated energy density also increases. However, this is at odds with the signature of blackbody radiation which, as frequency increases, increases to a peak then falls back. It is the failure of the Rayleigh-Jeans formula to correctly predict the signature of blackbody radiation that is known in physics as the ultraviolet catastrophe.

Where have I been?

Studies have had to take a back seat for the past few months, life has got in the way. I've moved house and had to do all the things that this entails, include a fair amount of re-decorating, I've been extremely busy at work, working toward the first flight of the product I'm working on. However, as I'm now much more settled in to the new house, and I'm going to be less busy at work, I should have some more time to study.

In fact, I have in the last couple of days read some of the first chapter of Eisberg & Resnick and came across a phrase that I don't think I ever came across while studying my degree (or perhaps I have just forgotten it), the 'ultraviolet catastrophe' - one of the reasons behind the need for QM, and as so I think I should do a more in depth blog post about it at some point in the future.

I really do need to do some maths, one cannot study physics in depth, without maths. More blog post on maths will follow also...

Review of The Theoretical Minimum - Chapter 1

This post is really the first post where I will use my blog for what I intent, and that is to review the things I have learned, or should I say relearned.

I have worked through Chapter 1 of Leonard Susskind first book in his "Theoretical Minimum" series. The aim of these books, along with his lecture videos, is to give the reader the minimum amount of physics knowledge to understand cutting edge physics. The first book covers classical physics and in the first chapter he sets out a number of topics. These include a description of what is meant by classical physics, a description of simple dynamical systems and their space-of-states,  dynamical laws which are allowable along with those that are not, how cycles within a systems space-of-states lead to conservations laws and finally how the initial conditions of system can never be know with infinite accuracy and therefore measurements carried out upon a system will always be subject to uncertainty.

What is Classical Physics?

Susskind sets out that classical physics/mechanics is used to describe physical phenomena for which a quantum uncertainties need not be accounted for. These include Newton's Laws of motion, Maxwell's and Faradays laws of electromagnetism, and Einstein's Special and General theory's of Relativity.

He also alludes that the job of classical mechanics is to predict the future. However, to predict the future every thing about a system at a given point in time needs to be known and how the system will change with time. He also sets out that the laws by which systems change with time must be deterministic and reversible, that is not only must they be able to predict the future, they must also be able to be used to determine what happened in the past.

Simple Dynamical Systems and Space of States

Two types of system are set out, where is system is simply a collection of objects:

• Closed system - either the entire universe or a collection of objects that are some remote that they behave as if nothing else exists

• Open system - A collection of objects which are open to external influence.

What is meant by deterministic and reversible laws are set out using some very elementary examples of systems. A coin which is affixed to a table, which obviously can't change state, as its space of state is very narrow, containing just the one state.  The law which describes how this system changes with time is both perfectly deterministic and reversible. The coin remains in the same state for all time, it has no choice.

A coin that is free to flip has a slightly wider space of states, that is, it has two states which is either heads or tails. There are many laws which could be set out to define how this system evolves with time however, two of the simplest are used. The first is if the coin starts at heads, it flips to tails, and if it is tails it flips to heads. The second is if the coin starts at tails, it flips to heads and if it is heads it flips to tails. (These two laws are in fact the same)

The laws which describe the time evolution of both of the above systems are perfectly deterministic and perfectly reversible, if the state of the coin is known at any point in time then the law(s) can be used to determine what will happen in the future or what has happened in the past with absolute certainty.

The concepts from the two 'coin' systems above are then expanded to include six sided dice, that is a system which has six states. Numerous dynamical laws could be use to describe the evolution of this system, for example a simple cyclic law where the dice cycles though sides 1 to 6 in order and then back to 1.

Or a cycle for example 1 to 3 to 2 to 6 to 4 to 5 and back to 1. This second cycle is in fact the same as the first as each in the state in the second cycle could simply be relabelled  to arrive at the first. However, here multiple cycles within a system is introduced. For example, two cycles - 1 to 2 to 3 and back to 1, and 4 to 5 to 6 and back to 4 - or even three cycles - 1 to 2 and back to 1, 3 to 4 and back to 3, and 5 to 6 and back to 6. The point is that even with multiple cycles within the space of states, the law which describes the whole system is perfectly deterministic and reversible - if the system is in any one of the states, then the next or previous state can be determined from the law.

Laws not Allowed

Examples of the types of laws that are not allowed are also given using simple systems similar to those used above. For example a three state system where the system cycles from 1 to 2 to 3 and back to 2. This system at first glance appears to be deterministic, however, if this cycle is reversed it leads to a problem, in that it is not clear which state is next if the system is in state 2, should it be 1 or 3? Also if the system is in state 1, which state is next? Therefore this law is deterministic, however it is not reversible. Laws of this type violate one of the central cannons of physics and that is the conservation of information. The information about which state the system starts in is lost.

Infinite Space of States and Conservation Laws

More realistic systems obviously have an infinite space of states, however, cycles within such systems can and do exist. In fact, such cycles are equivalent to quantities which are conserved, and directly lead to conservation laws

Precision

Finally it is pointed out that it is not possible to measure the initial conditions of the system with infinite accuracy, therefore for any set of measurements carried out on a system there will always be uncertainly in the prediction of the outcome of the system even if the dynamical law that describes the system of interest is known.

That's it for chapter 1. The next I shall review from this book is interlude 1, a section on Spaces, Trigonometry and Vectors.

Gravitational Waves Detected

With today's announcement of the detection of gravitational waves and the discovery of the Higg's Boson a couple of years ago, there is no better time to study physics!

My book list and tomorrow's announcement

As I said in my first post, I have a number of physics text books which I aim to work through. Below is the order in which I will proceed through them

Introduction to Classical Mechanics, French and Ebison
Electricity and Magnetism, Duffin
Electromagnetism, Grant and Phillips
Equilibrium Thermodynamics, Adkins
Properties of Matter, Flowers and Mendoza
Solid State Physics, Blakemore
Physics of Vibrations and Waves, Pain
Particle Physics, Martin and Shaw
Statistical Physics, Mandl
Special Relativity, French
Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles, Eisberg & Resnick

Those should keep me quite for some months to come.

Tomorrow I am eagerly awaiting an announcement from the LIGO team, who are searching for Gravitation waves. Maybe they've observed them, maybe not. If they have, maybe Einstein's theory of relativity will be finally promoted from being just a theory.

What an exciting time to be a physicist